9.1 베타 이해하기
투자자들이라면 누구나 한 번은 베타(Beta)라는 용어를 들어봤을 것입니다.
기본적으로 주식시장의 움직임은 개별 주식의 수익률에 가장 크게 영향을 주는 요소일 수밖에 없습니다.
아무리 좋은 주식도 주식시장이 폭락한다면 같이 떨어지며, 아무리 나쁜 주식도 주식시장이 상승한다면 대부분 같이 오르기 마련입니다.
개별 주식이 전체 주식시장의 변동에 반응하는 정도를 나타낸 값이 베타입니다.
베타가 1이라는 뜻은 주식시장과 움직임이 정확히 같다는 뜻으로서 시장 그 자체를 나타냅니다. 베타가 1.5라는 뜻은 주식시장이 수익률이 +1%일 때 개별 주식의 수익률은 +1.5% 움직이며, 반대로 주식시장의 수익률이 -1%일 때 개별 주식의 수익률은 -1.5% 움직인다는 뜻입니다.
베타값 = 회귀계수
반면 베타가 0.5라면 주식시장 수익률의 절반 정도만 움직이게 됩니다.
표 9.2: 베타에 따른 개별 주식의 수익률 움직임베타주식시장이 +1% 일 경우주식시장이 -1% 일 경우
| 0.5 | +0.5% | -0.5% |
| 1.0 | +1.0% | -1.0% |
| 1.5 | +1.5% | -1.5% |
이처럼 베타가 큰 주식은 주식시장보다 수익률의 움직임이 크며, 반대로 베타가 낮은 주식은 주식시장보다 수익률의 움직임이 작습니다.
따라서 일반적으로 상승장이 기대될 때는 베타가 큰 주식에, 하락장이 기대될 때는 베타가 낮은 주식에 투자하는 것이 좋습니다.
생각의 흐름
베타값을 측정하여 하면 종목선정에 도움을 받을 수 있다.
베타값을 어떻게 측정할 것인가?
알아야 하는 지식과 도구는?
상승장과 하락장을 어떻게 기대하나
어떻게 실전에 적용하나
주식시장에서 베타는 통계학의 회귀분석모형에서 기울기를 나타내는 베타와 정확히 의미가 같습니다.
회귀분석모형은 �=�+�� 형태로 나타나며, 회귀계수인 �는 �의 변화에 따른 �의 변화의 기울기입니다.
이를 주식에 적용한 모형이 자산가격결정모형(CAPM: Capital Asset Pricing Model)(Sharpe 1964)이며, 그 식은 다음과 같습니다.
회귀분석모형:�=�+��자산가격결정모형:��=��+��×[��−��]
먼저 회귀분석모형의 상수항인 �에 해당하는 부분은 무위험 수익률을 나타내는 ��입니다. 독립변수인 �에 해당하는 부분은 무위험 수익률 대비 주식 시장의 초과 수익률을 나타내는 시장위험 프리미엄인 ��−��입니다. 종속변수인 �에 해당하는 부분은 개별주식의 수익률을 나타내는 ��이며, 최종적으로 회귀계수인 �에 해당하는 부분은 개별 주식의 베타입니다.
표 9.3: 회귀분석모형과 자산가격결정모형의 비교구분회귀분석모형자산가격결정모형
| 상수항 | a | �� (무위험 수익률) |
| 독립변수 | x | ��−�� (시장위험 프리미엄) |
| 종속변수 | y | �� (개별주식의 수익률) |
| 회귀계수 | b | �� (개별주식의 베타) |
통계학에서 회귀계수는 �=���(�,�)��2 형태로 구할 수 있으며, �와 �에 각각 시장수익률과 개별주식의 수익률을 대입할 경우 개별주식의 베타는 ��=�(�,�)×���� 형태로 구할 수 있습니다. 그러나 이러한 수식을 모르더라도 R에서는 간단히 베타를 구할 수 있습니다.
9.1.1 베타 계산하기
베타를 구하는 방법을 알아보기 위해 주식시장에 대한 대용치로 KOSPI 200 ETF, 개별주식으로는 전통적 고베타주인 증권주를 이용하겠습니다.
library(quantmod)
library(PerformanceAnalytics)
library(magrittr)
symbols = c('102110.KS', '039490.KS')
getSymbols(symbols)## [1] "102110.KS" "039490.KS"prices = do.call(cbind,
lapply(symbols, function(x)Cl(get(x))))
ret = Return.calculate(prices)
ret = ret['2016-01::2018-12']- KOSPI 200 ETF인 TIGER 200(102110.KS), 증권주인 키움증권(039490.KS)의 티커를 입력합니다.
- getSymbols() 함수를 이용하여 해당 티커들의 데이터를 다운로드 받습니다.
- lapply() 함수 내에 Cl()과 get()함수를 사용하여 종가에 해당하는 데이터만 추출하며, 리스트 형태의 데이터를 열의 형태로 묶어주기 위해 do.call() 함수와 cbind() 함수를 사용해 줍니다.
- Return.calculate() 함수를 통해 수익률을 계산해 줍니다.
- xts 형식의 데이터는 대괄호 속에 [‘시작일자::종료일자’]와 같은 형태로, 원하는 날짜를 편리하게 선택할 수 있으며, 위에서는 2016년 1월부터 2018년 12월 까지 데이터를 선택합니다.
rm = ret[, 1]
ri = ret[, 2]
reg = lm(ri ~ rm)
summary(reg)##
## Call:
## lm(formula = ri ~ rm)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.06890 -0.01296 -0.00171 0.01082 0.09541
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.000400 0.000728 0.55 0.58
## rm 1.764722 0.091131 19.36 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0196 on 721 degrees of freedom
## (결측으로 인하여 8개의 관측치가 삭제되었습니다.)
## Multiple R-squared: 0.342, Adjusted R-squared: 0.341
## F-statistic: 375 on 1 and 721 DF, p-value: <2e-16증권주를 대상으로 베타를 구하기 위한 회귀분석을 실시합니다.
자산가격결정모형의 수식인 ��=��+��×[��−��] 에서 편의를 위해 무위험 수익률인 ��를 0으로 가정하면, ��=��×��의 형태로 나타낼 수 있습니다. 이 중 ��는 독립변수인 주식시장의 수익률을 의미하고, ��는 종속변수인 개별 주식의 수익률을 의미합니다.
- 독립변수는 첫 번째 열인 KOSPI 200 ETF의 수익률을 선택하며, 종속변수는 두번째 열인 증권주의 수익률을 선택합니다.
- lm() 함수를 통해 손쉽게 선형회귀분석을 실시할 수 있으며, 회귀분석의 결과를 reg 변수에 저장합니다.
- summary() 함수는 데이터의 요약 정보를 나타내며, 해당 예시에서는 회귀분석 결과에 대한 정보를 보여줍니다.
회귀분석의 결과 중 가장 중요한 부분은 계수를 나타내는 Coefficients입니다. Intercept는 회귀분석의 상수항에 해당하는 부분으로서, 값이 거의 0에 가깝고 t값 또한 매우 작아 유의하지 않음이 보입니다. 우리가 원하는 베타에 해당하는 부분 은 �의 Estimate로서, 베타값이 1.76으로 증권주의 특성인 고베타주임이 확인되며, t값 또한 19.36로 매우 유의한 결과입니다. 조정된 결정계수(Adjusted R-square)는 0.34를 보입니다.
9.1.2 베타 시각화
이제 구해진 베타를 그림으로 표현해보겠습니다.
plot(as.numeric(rm), as.numeric(ri), pch = 4, cex = 0.3,
xlab = "KOSPI 200", ylab = "Individual Stock",
xlim = c(-0.02, 0.02), ylim = c(-0.02, 0.02))
abline(a = 0, b = 1, lty = 2)
abline(reg, col = 'red')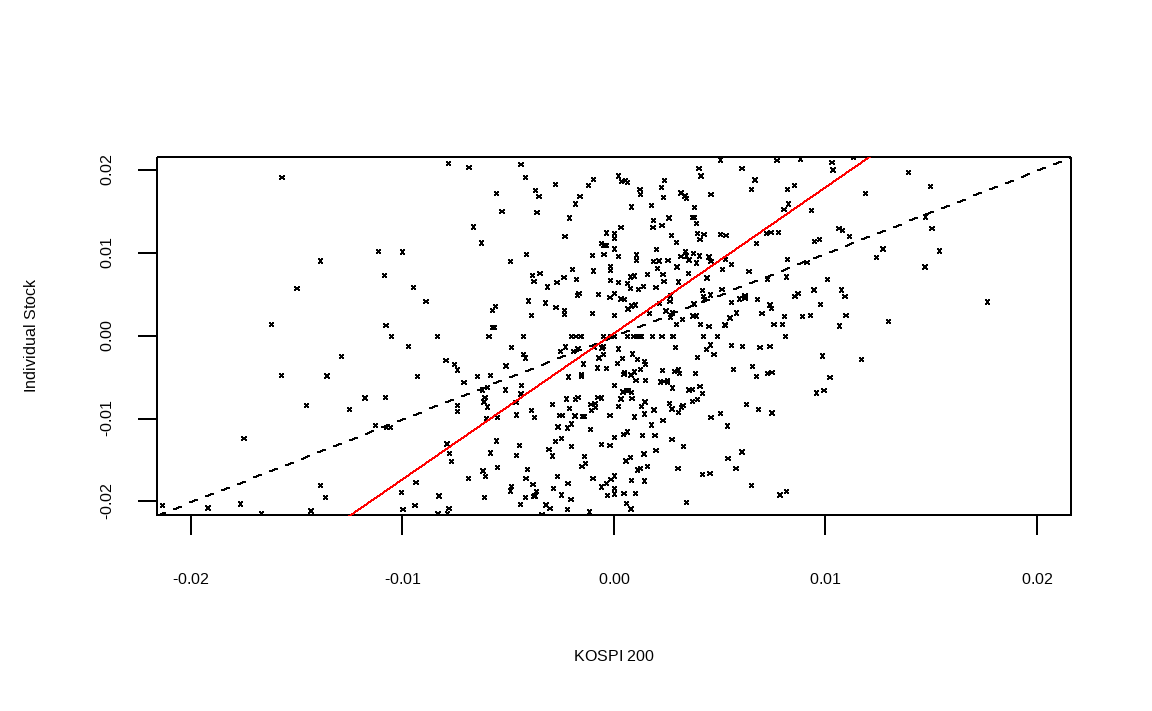
- plot() 함수를 통해 그림을 그려주며, x축과 y축에 주식시장 수익률과 개별 주식 수익률을 입력합니다. pch는 점들의 모양을, cex는 점들의 크기를 나타내며, xlab과 ylab은 각각 x축과 y축에 들어갈 문구를 나타냅니다. xlim과 ylim은 x 축과 y축의 최소 및 최대 범위를 지정해줍니다.
- 첫번째 abline()에서 a는 상수, b는 직선의 기울기, lty는 선의 유형을 나타냅니다. 이를 통해 기울기, 즉 베타가 1일 경우의 선을 점선으로 표현합니다.
- 두번째 abline()에 회귀분석 결과를 입력해주면 자동적으로 회귀식을 그려줍니다.
검은색의 점선이 기울기가 1인 경우이며, 주황색의 직선이 증권주의 회귀분석결과를 나타냅니다. 기울기가 1보다 훨씬 가파름이 확인되며, 즉 베타가 1보다 크다는 사실을 알 수 있습니다.
'재테크•투자•경제•주식' 카테고리의 다른 글
| python을 통한 CAPM 분석 (0) | 2023.07.12 |
|---|---|
| CAPM (자본자산 가격결정모형) (0) | 2023.07.12 |
| Chapter 1 퀀트 투자의 심장: 데이터와 프로그래밍 (0) | 2023.07.12 |
| dart-fss를 활용하여 기업 재무 재표 가져 오기 (0) | 2023.07.12 |
| chrome driver 다운로드 (0) | 2023.07.11 |

